
Pythagorean Theorem:
The Pythagorean Theorem is a fundamental principle in geometry that relates the lengths of the sides of a right-angled triangle. Named after the ancient Greek mathematician Pythagoras, this theorem is crucial in many areas of mathematics, physics, engineering, and everyday problem-solving.
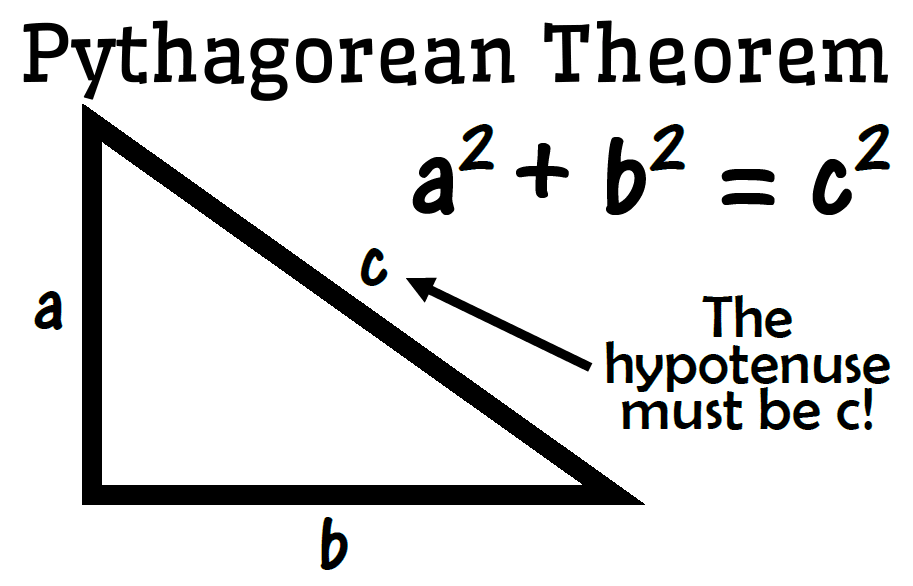
The Statement of the Pythagorean Theorem:
In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, this is expressed as: a2+b2=c2a^2 + b^2 = c^2
Where:
- aa and bb are the lengths of the legs (the two sides that form the right angle).
- cc is the length of the hypotenuse (the side opposite the right angle).
Key Terms:
- Right-Angled Triangle: A triangle where one of the angles is exactly 90∘90^\circ.
- Hypotenuse: The longest side of a right-angled triangle, opposite the right angle.
- Legs: The two sides that form the right angle in the triangle.
Example of Using the Pythagorean Theorem:
Suppose you have a right-angled triangle with legs of lengths 33 and 44. You can use the Pythagorean Theorem to find the length of the hypotenuse cc.
Given:
- a=3a = 3
- b=4b = 4
Using the Pythagorean theorem: a2+b2=c2a^2 + b^2 = c^2 32+42=c23^2 + 4^2 = c^2 9+16=c29 + 16 = c^2 25=c225 = c^2
Taking the square root of both sides: c=25=5c = \sqrt{25} = 5
So, the length of the hypotenuse cc is 5.
Applications of the Pythagorean Theorem:
- Distance Calculation: It’s used in determining the distance between two points in a coordinate plane. If you know the difference in the x and y coordinates of two points, you can use the theorem to find the straight-line distance between them. For example, if two points are at (x1,y1)(x_1, y_1) and (x2,y2)(x_2, y_2), the distance dd between them is: d=(x2−x1)2+(y2−y1)2d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}
- Trigonometry: The theorem is foundational in trigonometric identities and calculations, such as finding unknown angles or side lengths in triangles.
- Architecture and Engineering: It helps in designing structures, determining angles, and ensuring proper measurements for construction.
- Navigation: Pilots, sailors, and GPS systems use the Pythagorean theorem to calculate distances and determine the shortest path between two points.
Proof of the Pythagorean Theorem:
There are many ways to prove the Pythagorean Theorem. Here is one of the simplest proofs using geometric rearrangement (also known as the dissection proof):
- Start with a large square whose side length is a+ba + b.
- Inside this square, place four identical right-angled triangles, each with legs of length aa and bb, and hypotenuse cc.
- The area of the large square can be expressed in two ways:
- As the area of the square: (a+b)2(a + b)^2.
- As the sum of the areas of the four triangles and the smaller square formed by the hypotenuses: 4×12ab+c24 \times \frac{1}{2}ab + c^2.
- Equating the two expressions for the area, we get: (a+b)2=4×12ab+c2(a + b)^2 = 4 \times \frac{1}{2}ab + c^2
- Expanding both sides: a2+2ab+b2=2ab+c2a^2 + 2ab + b^2 = 2ab + c^2
- Cancel out the 2ab2ab terms: a2+b2=c2a^2 + b^2 = c^2
Thus, we arrive at the Pythagorean Theorem.
Generalizations and Extensions:
- Pythagorean Triples: These are sets of three positive integers aa, bb, and cc that satisfy the Pythagorean theorem. The most famous Pythagorean triple is 33, 44, and 55, but there are many others, like 55, 1212, and 1313, or 77, 2424, and 2525.
- In Non-Right-Angled Triangles: While the Pythagorean Theorem only applies to right-angled triangles, its concepts can extend to other geometric principles, like the law of cosines, which generalizes the idea for all triangles (not just right-angled ones).
Conclusion:
The Pythagorean Theorem is a fundamental and widely used principle in geometry, helping us solve problems related to distances, shapes, and many real-world applications. Whether it’s used in construction, navigation, or physics, its utility extends across many disciplines, making it one of the most important concepts in mathematics.

Leave a Reply