Symmetry:
Symmetry refers to a balanced and proportionate similarity found in two halves of an object, shape, or system, such that one half is a mirror image or a transformation of the other. In mathematics, symmetry is a concept that describes how an object or figure remains unchanged when subjected to certain transformations, such as reflection, rotation, or translation.
Symmetry is a fundamental concept in various fields including geometry, art, biology, physics, and chemistry. It plays a crucial role in the understanding of shapes, patterns, and the natural world.
Types of Symmetry:
- Reflective Symmetry (Mirror Symmetry):
- A figure has reflective symmetry if one half is a mirror image of the other. The figure can be divided into two equal parts that are reflections of each other.
- Example: A butterfly’s wings or the letter “A”.
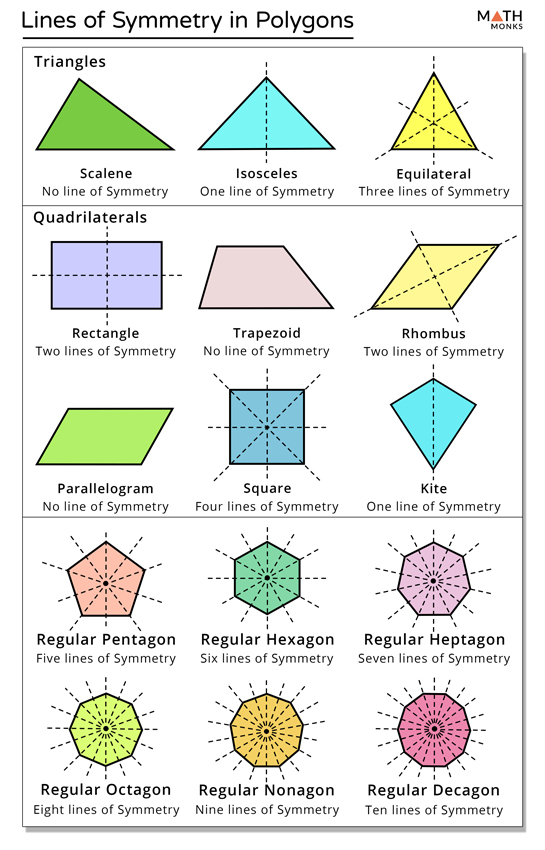
- Axis of Symmetry: The line that divides the shape into two mirror-image halves is called the axis of symmetry.
- Rotational Symmetry (Radial Symmetry):
- A shape has rotational symmetry if it can be rotated around a central point and still look the same at certain angles.
- Order of Symmetry: The number of times a shape matches itself during a 360° rotation is called the order of symmetry.
- Example: A star, wheel, or a flower.
- Translational Symmetry:
- A figure has translational symmetry if it can be moved (translated) along a straight line and still remain unchanged.
- This is common in patterns or tessellations where shapes repeat regularly.
- Example: A wallpaper pattern or a tile pattern.
- Glide Reflection Symmetry:
- Glide reflection symmetry occurs when an object is reflected over a line and then translated along the line of reflection.
- This combines both reflection and translation.
- Example: Some footprints in sand or certain tessellating patterns.
- Point Symmetry (Central Symmetry):
- A figure has point symmetry if every part of the object has a matching part at an equal distance from a central point but in the opposite direction.
- Example: A flower with petals arranged around a central point or the letter “N”.
Symmetry in Geometry:
- Symmetry in Polygons:
- Regular polygons (where all sides and angles are equal) have multiple lines of symmetry. For example, an equilateral triangle has three lines of symmetry, a square has four, and a regular hexagon has six.
- Symmetry Groups:
- In geometry, symmetry can be categorized into symmetry groups based on how shapes can be transformed while preserving their structure. These include rotation, reflection, and translation groups. The mathematical study of symmetry groups is called group theory, which has important applications in chemistry, physics, and crystallography.
Symmetry in Nature:
Symmetry is prevalent in the natural world, where many biological structures and patterns exhibit symmetry. This is often associated with optimal organization and functionality for living organisms.
- Bilateral Symmetry: Most animals, including humans, exhibit bilateral symmetry, where the left and right halves of the body are mirror images of each other.
- Example: Humans, butterflies, and dolphins.
- Radial Symmetry: Some organisms, especially invertebrates like starfish and jellyfish, have radial symmetry, where their body parts are arranged around a central axis.
- Example: Starfish, flowers, and sea anemones.
- Spiral Symmetry: Patterns that follow a spiral shape, such as the arrangement of leaves or the growth of shells, are often symmetric in nature.
- Example: Pine cones, snail shells, and galaxies.
Symmetry in Art and Architecture:
- Classical Architecture: Many buildings, especially in the classical tradition, make extensive use of symmetry in their design. For example, the Parthenon in Athens and the Palace of Versailles in France are renowned for their symmetrical layout.
- Islamic Art: Islamic art frequently uses symmetry to create intricate and beautiful patterns, often found in tile work and mosaics.
- Renaissance Art: The Renaissance artists like Leonardo da Vinci and Michelangelo incorporated symmetry into their artwork to create harmonious and proportionate compositions.
Mathematical Application of Symmetry:
- Symmetry in Algebra and Functions:
- Functions and equations can exhibit symmetry in their graphs. For instance:
- Even Functions: Functions that have reflection symmetry about the y-axis. For example, f(x)=x2f(x) = x^2 is symmetric because f(−x)=f(x)f(-x) = f(x).
- Odd Functions: Functions with point symmetry about the origin. For example, f(x)=x3f(x) = x^3 has the property that f(−x)=−f(x)f(-x) = -f(x).
- Functions and equations can exhibit symmetry in their graphs. For instance:
- Symmetry in Group Theory:
- Group theory studies mathematical structures that capture the concept of symmetry. A group is a set of elements with a binary operation that satisfies four fundamental properties: closure, associativity, identity, and invertibility. Symmetry groups help describe the symmetries of objects in both abstract and applied contexts (e.g., molecules, crystals).
- Symmetry in Crystallography:
- Crystals often exhibit symmetrical properties that can be described by group theory. The symmetrical arrangement of atoms in a crystal lattice determines many of the crystal’s physical properties.
Applications of Symmetry:
- Physics: Symmetry plays a fundamental role in physics, especially in theories of the universe, where symmetries in physical laws help explain conservation laws (like conservation of energy, momentum, etc.). The Standard Model of particle physics is based on symmetries in nature.
- Chemistry: In chemistry, molecular symmetry is crucial for understanding the properties of molecules, their reactivity, and even their spectroscopic behavior.
- Engineering and Robotics: Symmetry is used in designing mechanical systems, from engine parts to robots, where components are often designed to be symmetrical for balance and efficiency.
Summary:
Symmetry is a concept that finds its application across many fields, including geometry, biology, art, physics, and engineering. It refers to the balanced and proportional arrangement of parts in an object or pattern. In mathematics, symmetry is studied through transformations like reflections, rotations, and translations. Symmetry helps us understand both the natural world and the design of structures, and it has practical applications in fields ranging from molecular chemistry to architectural design.
By recognizing symmetry, we can solve problems, create aesthetically pleasing designs, and better understand the patterns that govern the universe.

Leave a Reply